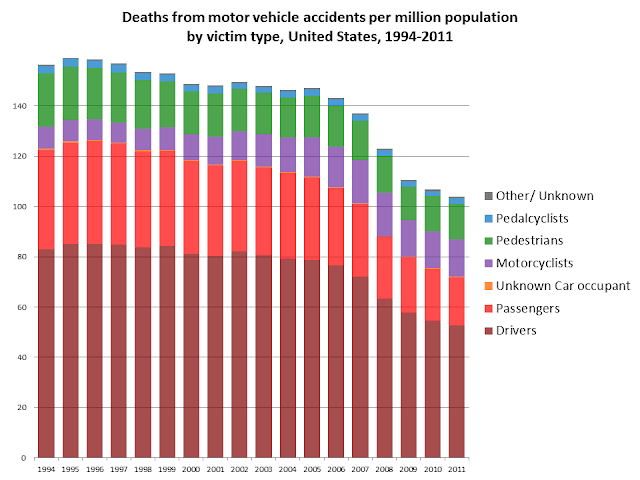
Every once in a while, I like to see what's going on with motor vehicle accidents. It turns out there's a lot going on. This data is from the Fatal Accident Reporting System. I haven't done anything special with it, just graphed the rather bland spreadsheet there on the home page.
The other thing that jumps out at me is the increase in the number of motorcyclists killed on the roads (the purple bars), and perhaps a decline in pedestrian deaths (green bars), and certainly a decline in passenger deaths (bright red bars).
The timing of the precipitous drop in 2008 and 2009 certainly suggests a connection to the recession - fewer vehicles on the roads = fewer deaths. That decline in vehicles would presumably come from three sources: fewer trucks delivering goods, fewer commuters, and fewer errands and pleasure trips. But why would there be more motorcyclist deaths? Perhaps the aging of the baby boom generation? And I haven't got a clue about why there would be fewer pedestrian deaths. It would be interesting to see whether the decline in pedestrian deaths is also linked to the 2008-2009 drops - and could that be attributed to fewer commuters? Or fewer errand and pleasure trips? The drop in passenger deaths seems to be pretty strongly linked to the recession - so is that about less car-pooling among the remaining commuters?
At any rate, graphing the number of deaths is a bit misleading, because the population keeps growing.
So, when you divide the number of deaths by the population (and multiply by 1,000,000), the peak year isn't 2005, but 1995. Actually, if you trace these trends back, the peak year on a per population basis is some time back in the 1920's, when cars were just mowing people down left and right, with very little effort to make the vehicles, the roads, or the drivers safer. What you see in the long term trends is a long slow decline in motor vehicle death rates, followed by a rapid decline in the 1970's, linked to that decade's recession, and also the high price of gas (much much higher than today once you take inflation into account), speed limit restrictions, the imposition of seat belts, investments in improved road infrastructure (guardrails etc.), and a radical shift in how we viewed drinking and driving. The slower decline continued in the 1980's through the late 2000's, especially due to air bags, improved vehicle construction, lighter vehicles that do less damage to others, and continuing trends in driver, vehicle, and road infrastructure safety. But that drop in 2008/2009 is still really dramatic, and I have to wonder if it can all be attributed to the recession.
Presumably, if the decline is due to the recession, it should be directly related to how many vehicles are on the roads. So, if you divide the deaths by 'vehicle miles traveled' instead, it should smooth out the trend...
And that seems to be the case. The long trend towards lower deaths per mile traveled dominates, but there is still an extra bump in 2008/2009, suggesting that the recession not only reduced the number of miles traveled, but also made the miles traveled safer, especially for passengers and pedestrians.
So, as we climb out of the recession, I'd expect to see the number (and rates) of motor vehicle deaths increase a litttle bit, maybe as high as 120 per million residents per year or 12 per billion miles traveled, and then continue the long slow decline.
So, here's another example of major improvements in health being made. Not as sexy a story as the latest fad in diet, but it's good to be reminded once in a while about what's going right.